SOAL
1. Simulasikan dengan
matlab suatu aplikasi Algoritma Genetik dibidang teknik elektro dari suatu
artikel/Tugas Akhir.
2. Simulasikan dengan
matlab suatu aplikasi Fuzzy dibidang teknik elektro dari suatu dari suatu
artikel/Tugas Akhir.
3. Simulasikan dengan matlab suatu aplikasi
JST/Fuzzy/Algoritma Genetik dibidang teknik elektro dari suatu artikel sesuai
judul Tugas Besar yang anda buat. Berikan saran untuk perbaikan artikel dan
realisasikannya menggunakan matlab.
JAWAB
1. Link
Artikel/Tugas Akhir : https://repository.its.ac.id/46169/1/2215105047-Undergraduate_Thesis.pdf
Listing
Program :
% Parameter Motor DC
J
= 0.01; % Inersia rotor (kg.m^2)
b
= 0.1; % Koefisien friksi (N.m.s)
K
= 0.01; % Konstanta elektromotif (V/rad/s)
R
= 1; % Resistansi (Ohm)
L
= 0.5; % Induktansi (H)
%
Fungsi Transfer Motor DC
num
= K;
den
= [(J*L) (J*R + b*L) (b*R + K^2)];
motor_tf
= tf(num, den);
%
Kontroler PID awal
Kp
= 1; Ki = 1; Kd = 1;
pid_controller
= pid(Kp, Ki, Kd);
%
Sistem Loop Tertutup Awal
closed_loop_sys
= feedback(pid_controller * motor_tf, 1);
%
Simulasi Respons Step Awal
figure;
step(closed_loop_sys);
title('Respons
Step dengan Parameter PID Awal');
grid
on;
%
Fungsi Objektif untuk Optimasi GA
objective_function
= @(x) pid_performance(x, motor_tf);
%
Batas Parameter PID
lb
= [0, 0, 0]; % Batas bawah
ub
= [10, 10, 10]; % Batas atas
%
Optimasi dengan GA
options
= optimoptions('ga', 'Display', 'iter', 'MaxGenerations', 100);
[opt_params,
~] = ga(objective_function, 3, [], [], [], [], lb, ub, [], options);
%
Parameter Optimal
Kp_opt
= opt_params(1);
Ki_opt
= opt_params(2);
Kd_opt
= opt_params(3);
%
Kontroler PID Optimal
optimal_pid_controller
= pid(Kp_opt, Ki_opt, Kd_opt);
optimal_closed_loop_sys
= feedback(optimal_pid_controller * motor_tf, 1);
%
Simulasi Respons Step Optimal
figure;
step(optimal_closed_loop_sys);
title('Respons
Step dengan Parameter PID Optimal');
grid
on;
%
Fungsi Evaluasi Kinerja
function
performance = pid_performance(params, motor_tf)
Kp = params(1); Ki = params(2); Kd =
params(3);
pid_controller = pid(Kp, Ki, Kd);
closed_loop_sys = feedback(pid_controller *
motor_tf, 1);
% Respons Step
[y, t] = step(closed_loop_sys);
overshoot = max(y) - 1;
settling_time = find(t >= 2 & abs(y
- 1) <= 0.02, 1, 'first');
% Penalti Kinerja
performance = overshoot^2 +
settling_time^2;
end
Video :
2. Link
Artikel/Tugas Akhir : https://lib.unnes.ac.id/27779/1/5301409025.pdf
Listing Program :
%
Parameter Sistem Suhu
C
= 1000; % Kapasitas panas ruangan (J/°C)
R
= 0.01; % Resistansi termal (°C/W)
Tamb
= 25; % Suhu lingkungan (°C)
%
Fungsi Transfer Sistem Suhu
num
= [1/(C*R)];
den
= [1 1/(C*R)];
temp_tf
= tf(num, den);
%
Simulasi Respons Step Awal
figure;
step(temp_tf);
title('Respons
Step Sistem Suhu Ruangan');
grid
on;
%
Membuat Sistem Fuzzy
fis
= mamfis('Name', 'TemperatureControl');
%
Variabel Input: Error Suhu
fis
= addInput(fis, [-5 5], 'Name', 'Error');
fis
= addMF(fis, 'Error', 'gaussmf', [2 -2], 'Name', 'Negative');
fis
= addMF(fis, 'Error', 'gaussmf', [2 2], 'Name', 'Positive');
%
Variabel Output: Daya Pemanas
fis
= addOutput(fis, [0 1], 'Name', 'HeaterPower');
fis
= addMF(fis, 'HeaterPower', 'trimf', [0 0.5 1], 'Name', 'Low');
fis
= addMF(fis, 'HeaterPower', 'trimf', [0.5 1 1], 'Name', 'High');
%
Aturan Fuzzy
ruleList
= [1 1 1 1; 2 2 1 1];
fis
= addRule(fis, ruleList);
%
Simulasi Sistem
error
= -3:0.1:3;
heater_power
= evalfis(fis, error);
%
Visualisasi Output
figure;
plot(error,
heater_power);
title('Output
Pengendali Fuzzy');
xlabel('Error');
ylabel('Daya
Pemanas');
grid
on;
Video :
3. Link
Artikel/Tugas Akhir : https://repository.its.ac.id/46169/1/2215105047-Undergraduate_Thesis.pdf
Listing
Program :
%
Parameter Motor DC (disesuaikan dengan sistem dalam artikel)
J
= 0.01; % Inersia rotor (kg.m^2)
b
= 0.1; % Koefisien friksi (N.m.s)
K
= 0.01; % Konstanta elektromotif (V/rad/s)
R
= 1; % Resistansi (Ohm)
L
= 0.5; % Induktansi (H)
%
Fungsi Transfer Motor DC
num
= K;
den
= [(J*L) (J*R + b*L) (b*R + K^2)];
motor_tf
= tf(num, den);
%
Fungsi Objektif untuk Optimasi GA
objective_function
= @(x) pid_performance(x, motor_tf);
%
Batas Parameter PID
lb
= [0, 0, 0]; % Batas bawah [Kp, Ki, Kd]
ub
= [10, 10, 10]; % Batas atas [Kp, Ki, Kd]
%
Optimasi menggunakan Algoritma Genetika
options
= optimoptions('ga', 'Display', 'iter', 'MaxGenerations', 100);
[opt_params,
~] = ga(objective_function, 3, [], [], [], [], lb, ub, [], options);
%
Parameter PID Optimal
Kp_opt
= opt_params(1);
Ki_opt
= opt_params(2);
Kd_opt
= opt_params(3);
%
Menampilkan Parameter Optimal
disp('Parameter
PID Optimal:');
disp(['Kp
= ', num2str(Kp_opt)]);
disp(['Ki
= ', num2str(Ki_opt)]);
disp(['Kd
= ', num2str(Kd_opt)]);
%
Kontroler PID Optimal
optimal_pid_controller
= pid(Kp_opt, Ki_opt, Kd_opt);
optimal_closed_loop_sys
= feedback(optimal_pid_controller * motor_tf, 1);
%
Simulasi Respons Step Optimal
figure;
step(optimal_closed_loop_sys);
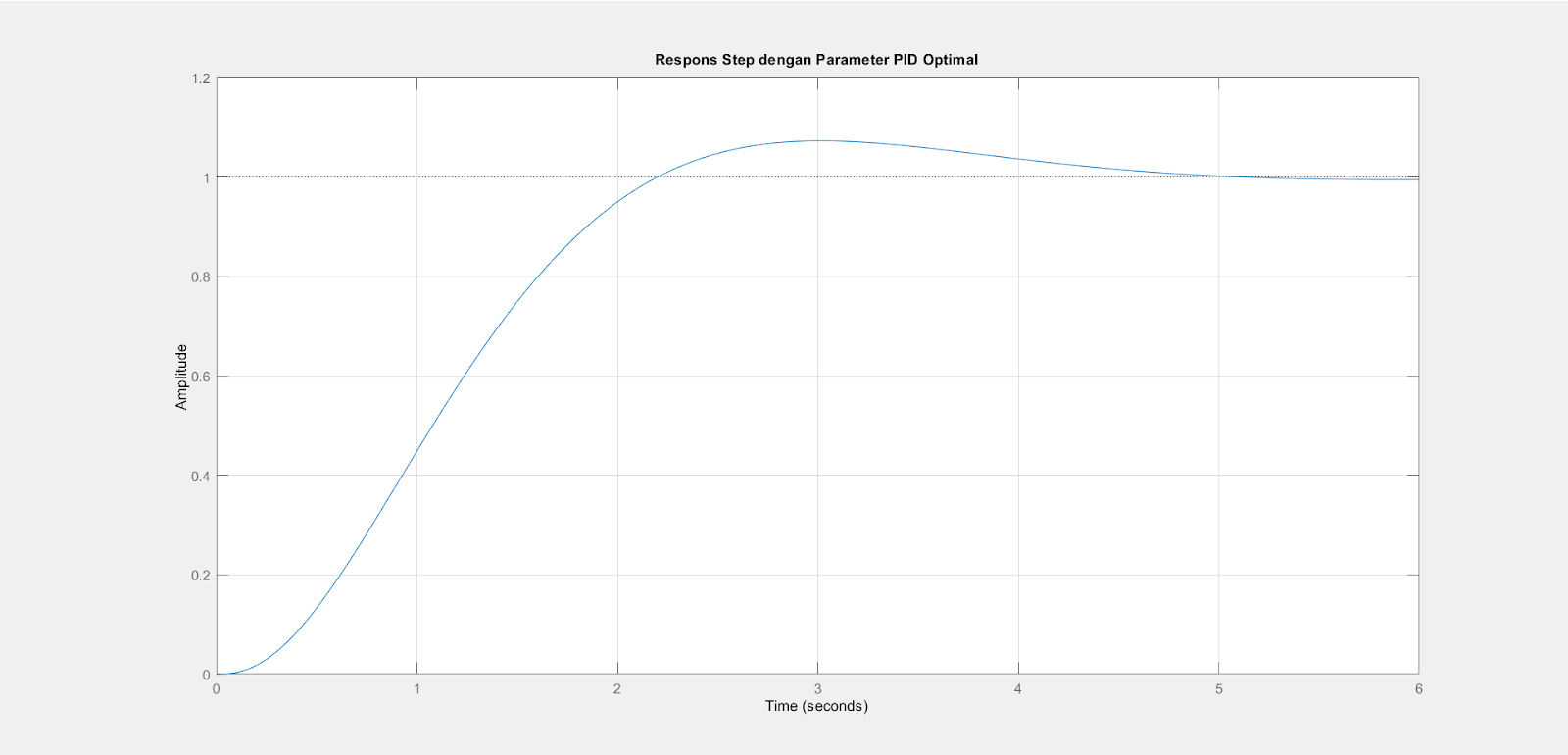
title('Respons
Step dengan Parameter PID Optimal');
grid
on;
%
Fungsi Evaluasi Kinerja PID
function
performance = pid_performance(params, motor_tf)
Kp = params(1); Ki = params(2); Kd =
params(3);
pid_controller = pid(Kp, Ki, Kd);
closed_loop_sys = feedback(pid_controller *
motor_tf, 1);
% Simulasi Respons Step
[y, t] = step(closed_loop_sys);
% Kriteria Kinerja: Overshoot dan Waktu
Stabil
overshoot = max(y) - 1;
settling_time_index = find(t >= 2 &
abs(y - 1) <= 0.02, 1, 'first');
if isempty(settling_time_index)
settling_time = max(t); % Jika tidak
stabil
else
settling_time = t(settling_time_index);
end
% Penalti Kinerja
performance = overshoot^2 +
settling_time^2;
end
Parameter PID Optimal:
Kp = 0.099237
Ki = 10
Kd = 0
Video :
Saran :
1. Parameter
Motor DC:
Artikel tidak mencantumkan nilai parameter motor DC secara eksplisit. Sebaiknya
parameter seperti inersia (J), koefisien friksi (b), konstanta elektromotif
(K), resistansi (R), dan induktansi (L) dijelaskan untuk memastikan simulasi
sesuai dengan sistem nyata.
2. Fungsi
Objektif:
Penjelasan tentang fungsi objektif dalam algoritma genetika sebaiknya
diperjelas, mencakup aspek seperti penalti terhadap overshoot, settling
time, dan stabilitas sistem.
3. Simulasi
Visualisasi:
Artikel dapat memperkaya pembahasan dengan menyertakan respons step
untuk parameter awal dan hasil optimasi, agar pembaca dapat melihat
perbandingan kinerja kontroler.
4. Validasi
Eksperimen:
Selain simulasi, validasi terhadap sistem nyata akan meningkatkan kredibilitas
hasil optimasi parameter PID.
Link
Download File
Program Klik Disini
Video Klik Disini




No comments:
Post a Comment