ABSTRAK
Saat
ini, pengendali Proportional Integral Derivative (PID) digunakan secara umum
untuk mendapatkan solusi optimum. Solusi dikatakan optimum apabila output di
kehidupan nyata sesuai dengan output yang telah ditentukan. Oleh karena itu,
pengendali adalah suatu hal yang dibutuhkan. Tantangan dalam menggunakan
pengendali adalah tuning parameter untuk mencari konstanta parameter PID
seperti Proporsional Gain (KP), Waktu Integral (KI) dan Waktu Derivatif (KD).
Untuk memaksimalkan kinerja motor DC, pengaturan pengendali PID yang tepat
merupakan hal yang sangat penting. Desain pengendali PID sebagai pengendali
motor DC sudah sering dilakukan. Penggunaan pengendali PID membutuhkan
pengaturan parameter yang tepat untuk mendapatkan kinerja yang optimal pada
motor. Metode yang umum dalam menentukan parameter pengendali PID adalah trial
and error. Namun hasil yang didapat tidak membuat pengendali PID optimal dan
justru akan merusak sistem. Oleh karena itu, penelitian ini menggunakan salah
satu metode penalaan parameter PID dengan menggunakan metode cerdas berbasis
Genetic Algorithm (Algoritma Genetik) untuk mengoptimasi dan menentukan
parameter yang tepat dari PID. Algoritma genetik adalah salah satu algoritma
yang menggunakan genetika sebagai model algoritmanya. Algoritma genetik
terinspirasi dari meniru proses seleksi alam, yaitu proses yang menyebabkan
evolusi biologis. Konsep inilah yang diadaptasi dan diterapkan dengan baik
untuk menala parameter PID. Penggunaan metode algoritma genetik dapat
memberikan hasil yang lebih baik pada setiap iterasinya. Hasil penelitian
menunjukkan bahwa overshoot yang dihasilkan karena adanya respon kecepatan
setelah penambahan PID adalah kurang dari 10%.
Kata Kunci: Pengendali
PID, algoritma genetik, motor DC.
BAB I
PENDAHULUAN
1.1. Latar
Belakang
Pengendali Proportional Integral Derivative (PID) merupakan pengendali konvensional yang masih banyak digunakan dalam dunia industri dibandingkan jenis kendali yang lebih modern. Pengendali PID memiliki 3 parameter, yaitu Konstanta Proporsional (KP), Konstanta Integral (KI), dan Konstanta Derivatif (KD). Tujuannya adalah untuk mendapatkan respon sistem yang optimal sesuai dengan spesifikasi perancangan yang diinginkan. Teknik penalaan PID ada beberapa metode, diantaranya metode Ziegler-Nichols, metode Fuzzy, dan metode Astrom-relay. Kebanyakan penalaan metode ini membutuhkan pengetahuan yang luas tentang sistem kontrol sehingga perlunya alternatif untuk otomatisasi penalaan dan praktisi yang tidak memerlukan pengetahuan sistem kontrol secara mendalam. Penggunaan pengendali PID membutuhkan pengaturan parameter yang tepat untuk mendapatkan kinerja yang optimal pada motor. Metode yang umum dalam menentukan parameter pengendali PID adalah trial and error. Namun hasil yang didapat tidak membuat pengendali PID optimal dan justru akan merusak sistem.
Pada penelitian ini,
Algoritma Genetik digunakan untuk menentukan parameter pengendali PID pada
motor DC sehingga pengendali dapat menghasilkan tanggapan sistem yang baik
(satisfactory response), khususnya pada kasus-kasus plant sample yang memiliki
orde tinggi. Algoritma Genetik merupakan suatu teknik optimasi berbasis evolusi
alam, yaitu melalui proses mutasi, pindah silang dan seleksi. Setelah
mendapatkan model sistem, Algoritma Genetik digunakan secara off-line dengan
simulasi untuk menentukan parameter pengendali PID. Hasil yang diperoleh saat
pengujian dan simulasi akan dirangkum dalam tabel pengaruh nilai parameter PID
dengan metode Algoritma Genetik.
1.2. Rumusan Masalah
1. Bagaimana Algoritma Genetik dapat digunakan untuk menyesuaikan parameter pengendali PID pada motor DC sehingga menghasilkan respons sistem yang optimal?
2. Apakah Algoritma Genetik mampu memberikan hasil yang lebih baik dibandingkan metode trial and error dalam penentuan parameter PID, terutama pada plant sample yang memiliki orde tinggi?
3. Seberapa efektif penerapan Algoritma Genetik dalam simulasi untuk menghasilkan parameter PID yang optimal pada motor DC?
1.3. Tujuan Penelitian
1. Mengembangkan
metode optimasi parameter PID menggunakan Algoritma Genetik untuk menghasilkan
respons sistem yang optimal pada motor DC.
2. Menganalisis
dan membandingkan hasil parameter PID yang diperoleh melalui Algoritma Genetik
dengan metode konvensional trial and error.
3. Menguji
efektivitas Algoritma Genetik dalam menyesuaikan parameter PID pada motor DC
melalui simulasi plant sample dengan orde tinggi.
1.4. Manfaat
Penelitian
1. Memberikan
alternatif metode penentuan parameter PID yang lebih otomatis dan akurat,
sehingga memudahkan praktisi yang kurang memahami sistem kontrol secara
mendalam.
2. Mengurangi
waktu dan usaha dalam proses penalaan parameter PID pada motor DC melalui
pendekatan Algoritma Genetik yang lebih efisien dibandingkan trial and error.
3. Menyediakan
kontribusi ilmiah dalam bentuk data dan hasil simulasi yang dapat menjadi acuan
dalam penerapan teknik optimasi pada sistem kontrol motor DC dan sistem kontrol
industri lainnya.
BAB II
TINJAUAN PUSTAKA
2.1. Pengendali PID
Pengendali
Proportional Integral Derivative (PID) adalah jenis pengendali umpan balik yang
paling banyak digunakan dalam industri, terutama untuk sistem dengan dinamika
yang relatif sederhana. Pengendali PID memiliki tiga parameter utama: konstanta
proporsional (Kp), konstanta integral (Ki), dan konstanta derivatif (Kd).
Ketiga parameter ini mempengaruhi respons sistem secara keseluruhan, seperti
kecepatan respons, stabilitas, dan tingkat osilasi (Ogata, 2010).
Menurut
Astrom dan Hagglund (2006), pengendali PID memiliki keunggulan dalam
kesederhanaan struktur dan kemampuannya untuk memberikan kinerja yang memadai
dalam beragam aplikasi. Namun, efektivitas pengendali PID sangat bergantung
pada akurasi parameter yang ditentukan. Pemilihan parameter yang tepat
seringkali dilakukan dengan teknik trial and error yang membutuhkan waktu dan
tidak menjamin hasil optimal.
2.2. Teknik Penalaan PID
Teknik
penalaan PID bertujuan untuk menentukan nilai optimal dari parameter Kp, Ki,
dan Kd agar sistem kontrol bekerja sesuai spesifikasi yang diinginkan. Salah
satu metode klasik yang banyak digunakan adalah metode Ziegler-Nichols, yang
diperkenalkan pada tahun 1942. Metode ini memberikan aturan penalaan berbasis
eksperimen, namun sering kali tidak cukup akurat untuk sistem dengan
karakteristik kompleks (Ziegler & Nichols, 1942).
Sebagai
alternatif, metode penalaan lain seperti metode Fuzzy Logic dan Astrom-Relay
telah dikembangkan untuk meningkatkan akurasi parameter PID (Astrom &
Hagglund, 1995). Akan tetapi, metode-metode ini tetap memerlukan pengetahuan
yang cukup mendalam tentang dinamika sistem, yang tidak selalu dimiliki oleh
praktisi di lapangan.
2.3. Algoritma Genetik untuk Optimasi PID
Algoritma
Genetik (Genetic Algorithm atau GA) adalah salah satu metode optimasi berbasis
teori evolusi yang bekerja dengan prinsip seleksi alamiah. Algoritma ini
menggunakan proses seperti seleksi, mutasi, dan crossover untuk menemukan
solusi optimal dari masalah tertentu (Goldberg, 1989). Dalam konteks pengendali
PID, Algoritma Genetik dapat digunakan untuk mengoptimalkan parameter Kp, Ki,
dan Kd tanpa memerlukan pengetahuan mendalam tentang karakteristik sistem
kontrol.
Beberapa
penelitian telah membuktikan keefektifan Algoritma Genetik dalam optimasi
parameter PID. Misalnya, penelitian oleh Rashid dan Hussain (2014) menunjukkan
bahwa GA dapat memberikan hasil penalaan PID yang lebih baik dibandingkan
metode konvensional dalam beberapa kasus tertentu, terutama pada sistem orde
tinggi yang kompleks. Dalam penelitian lain, Wahyudi dan Pranoto (2020)
menemukan bahwa penggunaan GA pada sistem kontrol motor DC meningkatkan
stabilitas dan kecepatan respons sistem.
2.4. Penggunaan Algoritma Genetik dalam
Sistem Motor DC
Motor
DC banyak digunakan dalam industri karena kemampuannya untuk menyediakan
kecepatan dan torsi yang stabil serta kontrol yang relatif mudah. Namun, untuk
memastikan performa yang optimal, parameter pengendali PID pada motor DC harus
disesuaikan dengan karakteristik beban dan kondisi operasi (Bolton, 2015).
Beberapa studi telah menggunakan Algoritma Genetik untuk optimasi pengendalian
pada motor DC dan menunjukkan peningkatan signifikan dalam performa sistem (Sun
et al., 2016).
Menurut
penelitian oleh Tan dan Zheng (2018), penggunaan Algoritma Genetik dalam tuning
PID pada motor DC berhasil mengurangi kesalahan steady-state dan mempercepat
waktu respon sistem. Hal ini menunjukkan bahwa GA memiliki potensi besar dalam
memperbaiki kualitas sistem kontrol pada berbagai jenis motor, termasuk motor
DC.
2.5. Simulasi dan Evaluasi Parameter PID
Dalam
aplikasi Algoritma Genetik pada tuning PID, simulasi sangat penting untuk
menguji efektivitas parameter yang diperoleh. Simulasi umumnya dilakukan secara
offline untuk memastikan bahwa hasil parameter tuning dari GA sesuai dengan
kondisi nyata tanpa harus melakukan eksperimen langsung pada hardware (Johnson
et al., 2017). Metode ini memberikan gambaran awal performa sistem dan
mengurangi risiko kerusakan perangkat keras akibat penalaan yang kurang tepat.
BAB III
METODE PENELITIAN
Dalam
desain sistem ini, digunakan algoritma genetik untuk menentukan parameter
pengendali PID. Diagram blok pengendali PID dengan fungsi alih ditunjukkan pada
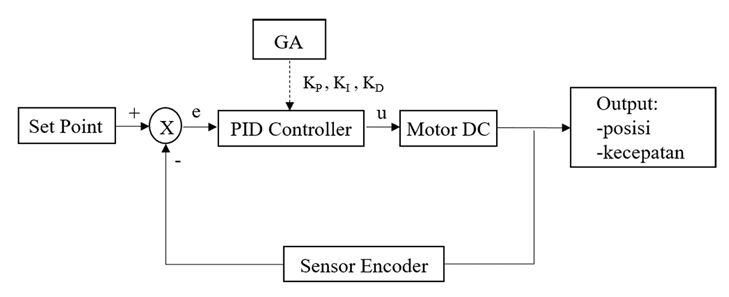
Gambar 1.
Gambar
1 menunjukan bahwa input sistem berupa sebuah tuning parameter PID dengan
menggunakan Algoritma Genetik (GA) sebagai metode pengendalinya untuk mencari
konstanta parameter PID. Plant yang digunakan ialah sebuah sistem kendali umpan
balik yang keluarannya berupa sebuah kecepatan dari motor DC.
3.2.
Diagram Blok Hardware
Selain
adanya diagram blok tuning pengendali PID, pada penelitian ini dibuat juga
diagram blok hardware serta wiring hardware untuk menunjukkan penjelasan
perangkat keras yang digunakan. Diagram blok hardware ditunjukkan pada Gambar
2.
Pada
Gambar 2 diperlihatkan diagram blok pemodelan motor DC yang menggunakan board
Arduino Uno R3 sebagai pengendali sistem. Board Arduino mendapat supply
tegangan dari power supply yang sudah disiapkan sebesar 12 volt yang disalurkan
pada driver motor untuk menggerakkan motor DC. Selanjutnya gerakan putar motor
DC akan dicatat oleh encoder yang akan diberikan pada Arduino Uno R3 agar dapat
dilihat hasilnya pada software Arduino Ide pada menu serial monitor dan serial
plotter.
3.3.
Diagram Pengkabelan Hardware
Wiring
diagram atau diagram pengkabelan dari sistem yang dibuat dapat dilihat pada
Gambar 3.
Perancangan
perangkat keras dibuat untuk mengontrol motor DC, dan driver motor untuk
melihat respon sistem dan juga sebagai alat pengambilan data yang diperlukan
untuk memodelkan motor DC menggunakan pendekatan pemodelan identifikasi sistem,
data yang akan digunakan berupa tegangan dan kecepatan putar motor DC.
3.4.
Algoritma Genetik
Prosedur
Algoritma Genetik digambarkan dalam bentuk flowchart yang ditunjukkan pada
Gambar 4.
Berdasarkan
Gambar 4, standar utama Algoritma Genetik mencakup empat operator sebagai
berikut:
a.
Seleksi GA adalah operasi seleksi yang akan memilih solusi induk.
b.
Selama fase reproduksi GA, individu dipilih dari populasi dan direkombinasi,
menghasilkan keturunan yang pada gilirannya akan terdiri dari generasi
berikutnya.
c.
Crossover mengambil dua induk dan memotong string kromosom induk di beberapa
posisi yang dipilih secara acak, untuk menghasilkan dua segmen “kepala” dan dua
segmen “ekor”.
d.
Mutasi diterapkan pada setiap anak secara individual, setelah crossover.
HASIL DAN PEMBAHASAN
4.1.
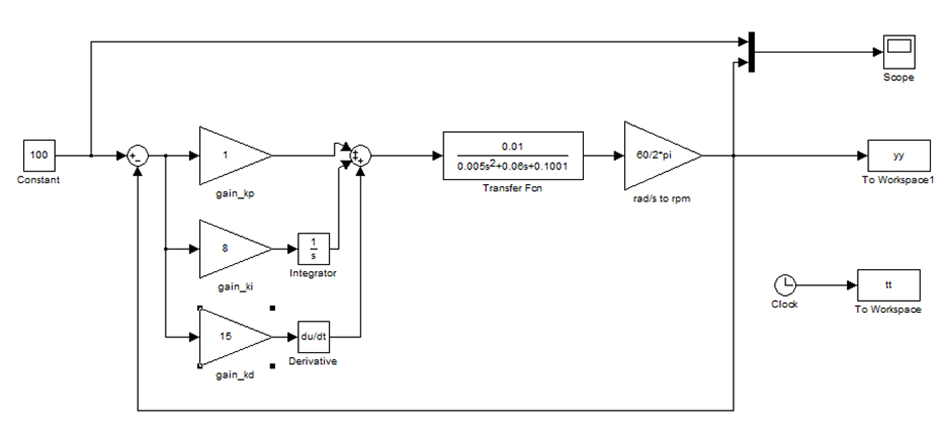
Pemilihan Model Transfer Function
Motor
DC Model TF Motor DC tersebut diambil dari jurnal, yaitu
4.2.
Pengujian menggunakan Metode Trial and Error
Pengujian dengan metode trial and error atau
metode coba-coba pada nilai KP, KI dan KD dilakukan untuk mengetahui
perbandingan parameter PID yang didapatkan. Pengujian dengan metode tersebut
menggunakan plant motor DC pada Matlab seperti ditunjukkan pada Gambar 5.
Hasil
dari pengujian menggunakan metode trial and error ini ditunjukkan pada Tabel 1.
Pengujian dilakukan sebanyak lima kali dengan hasil berupa grafik pada plant motor DC seperti yang ditunjukkan pada Gambar 6 dan Gambar 7.
Berdasarkan
pengujian yang dilakukan, diperoleh nilai overshoot yang sangat besar yaitu
85,6825% untuk Gambar 6 dan 49,2620% untuk Gambar 7. Nilai settling time yang
didapat bernilai NaN. NaN adalah singkatan dari Not a Number (bukan angka). NaN
ialah nilai tipe data numerik yang mewakili nilai yang tidak ditentukan atau
tidak terwakili, terutama dalam aritmatika titik-mengambang. Dalam pengujian
menggunakan metode trial and error ini menunjukkan bahwa semua percobaan yang
dilakukan bernilai NaN dan terjadi pada data settling time. Pengujian
menggunakan metode trial and error tidak efektif dalam mencari parameter PID
yang diinginkan.
4.3.
Pengujian menggunakan Metode Algoritma Genetik (GA)
Pengujian
menggunakan metode Algoritma Genetik dilakukan dengan tiga macam pengujian yang
dipengaruhi oleh fungsi Algoritma Genetik itu sendiri. Fungsi Algoritma Genetik
di antaranya adalah proses mutasi, proses pindah silang dan jumlah generasi
variasi. Proses pengujian dijalankan dengan Matlab.
4.3.1. Pengujian menggunakan GA
dengan Pengaruh Pmutasi
Pengaruh
Pmutasi dilakukan dengan proses memasukkan nilai Pmutasi 0,8 dan 1. Selanjutnya
memasukkan nilai Psilang 0,6 pada semua data yang dicobakan dan menggunakan
jumlah generasi 100. Hasil simulasi untuk transfer function motor DC pada
persamaan pemilihan model ditampilkan pada Gambar 8 dan Gambar 9.
Pengujian selanjutnya ialah memasukkan nilai parameter PID (KP, KI, KD) yang didapatkan dari hasil simulasi Pmutasi pada plant motor DC Matlab. Hasil yang ditampilkan dari pengujian tersebut berupa grafik yang ditunjukkan pada Gambar 10 dan Gambar 11.
Dari hasil simulasi Pmutasi 0,8 dan Pmutasi 1, diperoleh nilai overshoot yang sama, yaitu sebesar 0%. Hasil yang ditunjukkan pada grafik di atas bisa dianggap lebih baik dari grafik dengan metode trial and error. Akan tetapi, nilai overshoot tersebut belum tentu mutlak saat pengujian menggunakan alat. Hasil dari pengujian menggunakan metode GA dengan pengaruh Pmutasi ini ditunjukkan pada Tabel 2.
Dari hasil pengujian 2 ini diperoleh nilai overshoot 0 pada seluruh data. Overshoot yang didapatkan sudah optimal dengan nilai parameter PID yang sudah memenuhi syarat, yaitu KP ≥ KI ≥ KD.
4.3.2 Pengujian menggunakan GA dengan
Pengaruh Psilang
Pengaruh Psilang dilakukan dengan proses
memasukkan nilai Psilang 0,2; 0,4. Selanjutnya memasukkan nilai Pmutasi 0,6
pada semua data yang dicobakan dan menggunakan jumlah generasi 100. Hasil
simulasi untuk transfer function motor DC pada persamaan pemilihan model
ditampilkan pada Gambar 12 dan Gambar 13.
Pengujian
selanjutnya ialah memasukkan nilai parameter PID (KP, KI, KD) yang didapatkan
dari hasil simulasi Psilang pada plant motor DC Matlab. Hasil yang ditampilkan
dari pengujian tersebut berupa grafik yang ditunjukkan pada Gambar 14 dan
Gambar 15.
Hasil
yang diperoleh dari simulasi Psilang 0,2 memiliki nilai overshoot yang besar,
yaitu 36,1315%. Sedangkan simulasi Psilang 0,24 menghasilkan nilai overshoot
sebesar 0%. Hasil yang ditunjukkan pada grafik di atas bisa dianggap lebih baik
dari grafik dengan metode trial and error, tetapi belum lebih baik dari grafik
metode GA Pmutasi yang menampilkan grafik tanpa overshoot lebih banyak. Hasil
dari pengujian menggunakan metode GA dengan pengaruh Psilang ini ditunjukkan
pada Tabel 3.
Dari
hasil pengujian 3 ini diperoleh nilai overshoot 0 pada data nomor 2. Overshoot
yang didapatkan sudah optimal dengan nilai parameter PID yang sudah memenuhi
syarat, yaitu KP ≥ KI ≥ KD.
4.3.3 Pengujian menggunakan GA dengan
Pengaruh Jumlah Generasi Variasi
Pengaruh
jumlah generasi sangat menentukkan parameter PID, jumlah generasi ini tidak
mutlak harus lebih besar ataupun lebih kecil karena ditentukan dengan
pergerakan dari nilai fitness terbaik. Jumlah generasi yang digunakan pada
simulasi ini terdiri dari lima data, yaitu jumlah generasi 120 dan jumlah
generasi 150. Selanjutnya memasukkan nilai Pmutasi dan Psilang 0,6 pada semua
data yang dicobakan. Hasil simulasi untuk transfer function motor DC pada
persamaan pemilihan model ditampilkan pada Gambar 16 dan Gambar 17.
Pengujian
selanjutnya ialah memasukkan nilai parameter PID (KP, KI, KD) yang didapatkan
dari
hasil simulasi jumlah generasi variasi pada plant motor DC Matlab. Hasil yang
ditampilkan
dari
pengujian tersebut berupa grafik yang ditunjukkan pada Gambar 18 dan Gambar 19.
Hasil
yang diperoleh dari simulasi jumlah generasi 120 dan jumlah generasi 150
memiliki nilai overshoot yang sama, yaitu 0%. Hasil yang ditunjukkan pada
grafik di atas bisa dianggap lebih baik dari grafik dengan metode trial and
error dan grafik dengan metode GA Pmutasi karena menampilkan overshoot yang
lebih banyak. Akan tetapi, nilai overshoot tersebut belum tentu
mutlak
saat pengujian menggunakan alat. Hasil dari pengujian menggunakan metode GA
dengan
pengaruh
jumlah generasi variasi ini ditunjukkan pada Tabel 4.
4.4.
Pengujian Hardware
Hardware
yang digunakan pada pengujian tersebut ditunjukkan pada Gambar 20.
Pengujian
hardware dilakukan setelah proses pengujian 1 sampai pengujian 4 mendapatkan
hasil berupa 6 data nilai parameter PID (KP, KI, KD) menggunakan metode trial
and error dan GA. Kemudian data tersebut diuji pada alat yang telah dirancang
untuk mendapatkan hasil optimal yang sesuai dengan tujuan peneliti. Proses
pengujian hardware dijalankan dengan aplikasi Arduino dan untuk menampilkan
informasi respon sistem menggunakan Matlab. Hasil dari pengujian hardware ini
ditunjukkan pada Tabel 5.
Pengujian
hardware dilakukan sebanyak 8 kali sesuai dengan jumlah data dari pengujian
sebelumnya. Urutan dari pengujian tersebut sudah sesuai dengan pengujian 1
sampai 4. Hasil daripengujian hardware berupa grafik kecepatan motor DC yang
kemudian akan dibandingkan untuk mendapatkan nilai overshoot terkecil. Grafik
tersebut ditunjukkan pada Gambar 21 sampai Gambar 28.
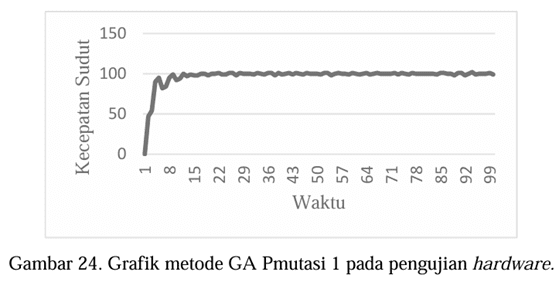
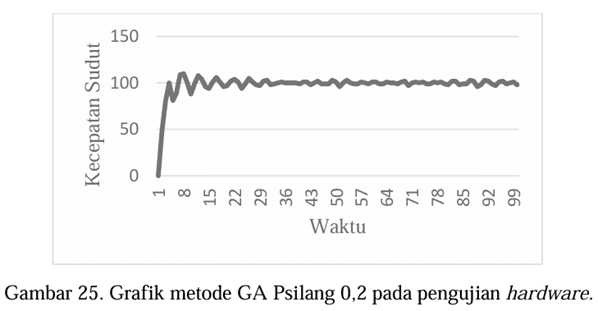
Dari
hasil pengujian hardware menggunakan kecepatan motor DC dengan parameter PID
sebagai input, dapat dilihat ada empat data yang sudah menampilkan overshoot
minimum 10%, yaitu Gambar 24 dengan nilai Pmutasi 1, Gambar 25 dengan nilai
Psilang 0,2, Gambar 26 dengan nilai Psilang 0,4 dan Gambar 27 dengan nilai
generasi 120. Tetapi data terbaik tersebut tidak dapat dilihat dari nilai
overshoot saja. Peneliti harus membandingkan nilai parameter PID yang
dihasilkan apakah sudah memenuhi syarat (KP ≤ KI ≤ KD) dan kecepatan yang
didapat sudah stabil (steady state) sampai data ke-100, serta tidak ada
kenaikan lonjakan yang signifikan ataupun undershoot yang dinilai kurang baik.
Temuan-temuan yang ditemukan pada keseluruhan percobaan ini dapat dilihat dari
nilai parameter PID yang didapat serta grafik yang ditampilkan. Ada dua data
pengujian terbaik dari segi nilai overshoot maupun nilai parameter PID yang
menjadi input, yaitu pada Gambar 24, parameter PID nya adalah KP = 3,7500; KI =
1,3184 dan KD = 0,2051. Untuk nilai overshoot = 2, undershoot = 0 dan untuk
waktu tunak (settling time) = 13,5 serta waktu naik (risetime) = 2,7872. Kemudian
Gambar 26, parameter PID nya adalah KP = 4,2090; KI = 1,2012 dan KD = 0,2539.
Untuk nilai overshoot = 2, undershoot = 0 dan untuk waktu tunak (settling time)
= 18 serta waktu naik (risetime) = 2,6462.
Listing
Program
BAB V
KESIMPULAN
Setelah
dilakukan penelitian dan mengolah data pada penelitian ini, algoritma Genetik
untuk penalaan parameter pengendali PID ini sudah menemukan solusi optimal
dengan overshoot di bawah 10%, dengan jumlah generasi 100 pada pengaruh Pmutasi
0,4 dan Pengaruh Psilang 0,8 serta pengaruh jumlah generasi variasi 120 dan
150. Metode algoritma genetik terbukti memberikan hasil sistem yang memiliki
waktu tunak lebih baik dan lonjakan maksimum yang lebih kecil dibandingkan
metode trial and error yang digunakan dalam simulasi. Proses pengujian hardware
dengan metode algoritma genetik pada motor DC dapat berjalan dengan baik,
sehingga didapatkan data terbaik berupa nilai overshoot di bawah 10% dan
parameter PID yang memenuhi syarat. Proses pengujian tersebut menghasilkan dua
data terbaik dengan nilai overshoot = 2 dan nilai parameter PID terbaik pada
Pmutasi 1 ialah KP = 3,7500; KI = 1,3184 dan KD = 0,2051 serta nilai parameter
PID terbaik pada Psilang 0,4 ialah KP = 4,2090; KI = 1,2012 dan KD = 0,2539.






















No comments:
Post a Comment